Remember how in math class, every fact was introduced intuitively & visually, and you never had to rote-memorize stuff without understanding them?

Yeah me neither. I'm considering writing a book titled: Math For People Who Have Been Scarred For Life By Math (or: Algebra in Pictures). It'd be the K-12 algebra book I wish I had as a kid: a book where all the facts are re-discovered from scratch, with beautiful visual intuition.

While outlining this book, I quickly realized: I don't know why some basic facts in algebra are true.

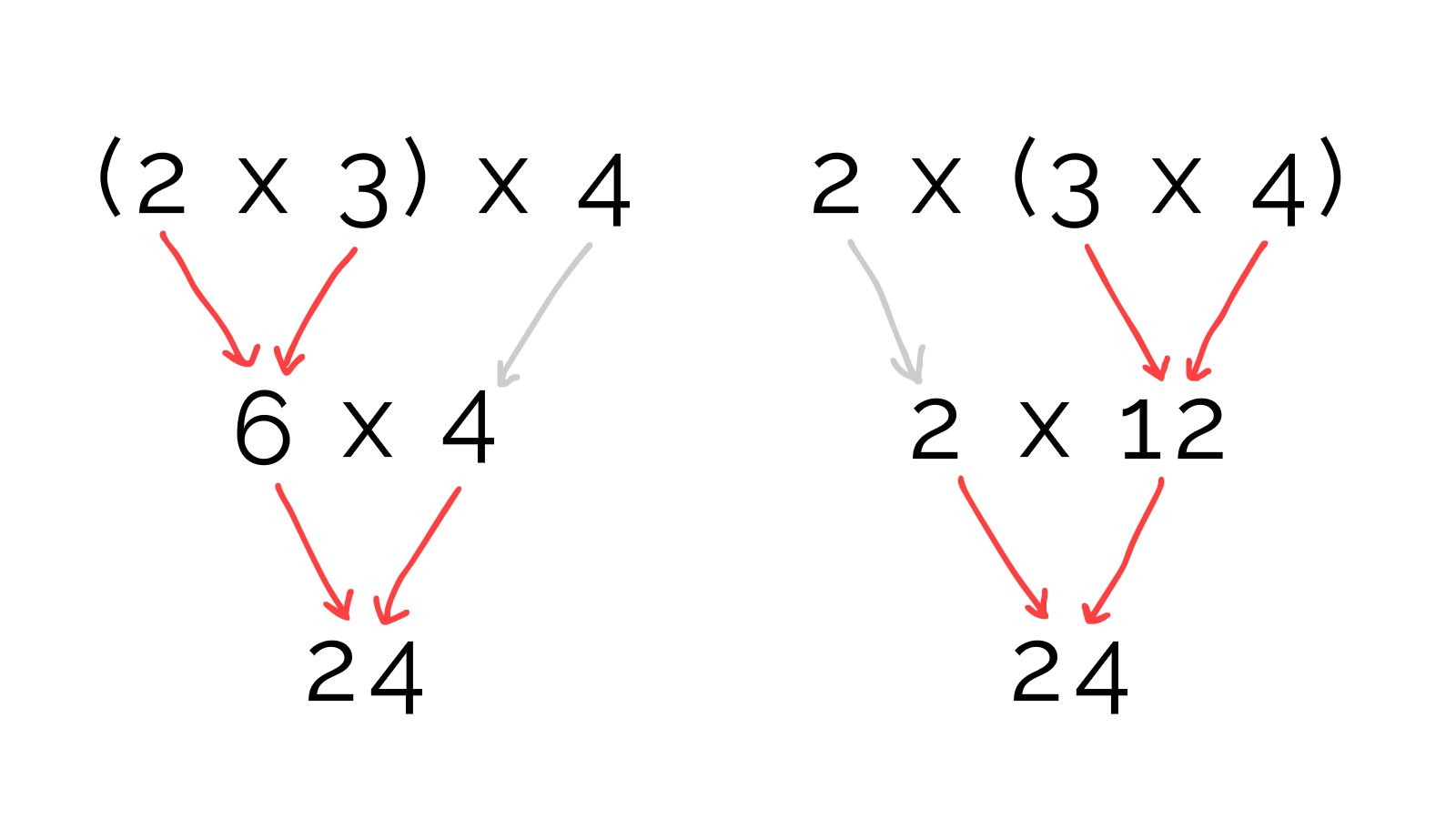
For example, I had no idea why brackets don't matter in multiplication. This fact is called "associativity": \((a \times b) \times c = a \times (b \times c)\).

[Yes, it's an "axiom", but why does this specific axiom hold for multiplying numbers?! Associativity isn't true for some operators! e.g. Subtraction: \((3 - 2) - 1 \neq 3 - (2 - 1)\).]

As far as I know, there does not already exist a published visual proof for why brackets don't matter (associativity) when multiplying whole numbers.

In contrast, there do already exist:

1. A classic visual proof for why order doesn't matter ("commutativity") in multiplying two numbers:

2. A visual proof for associativity in multiplying three numbers.^[1] (But it requires a 3D visualization, so it's impossible to visualize multiplying more than three numbers.)

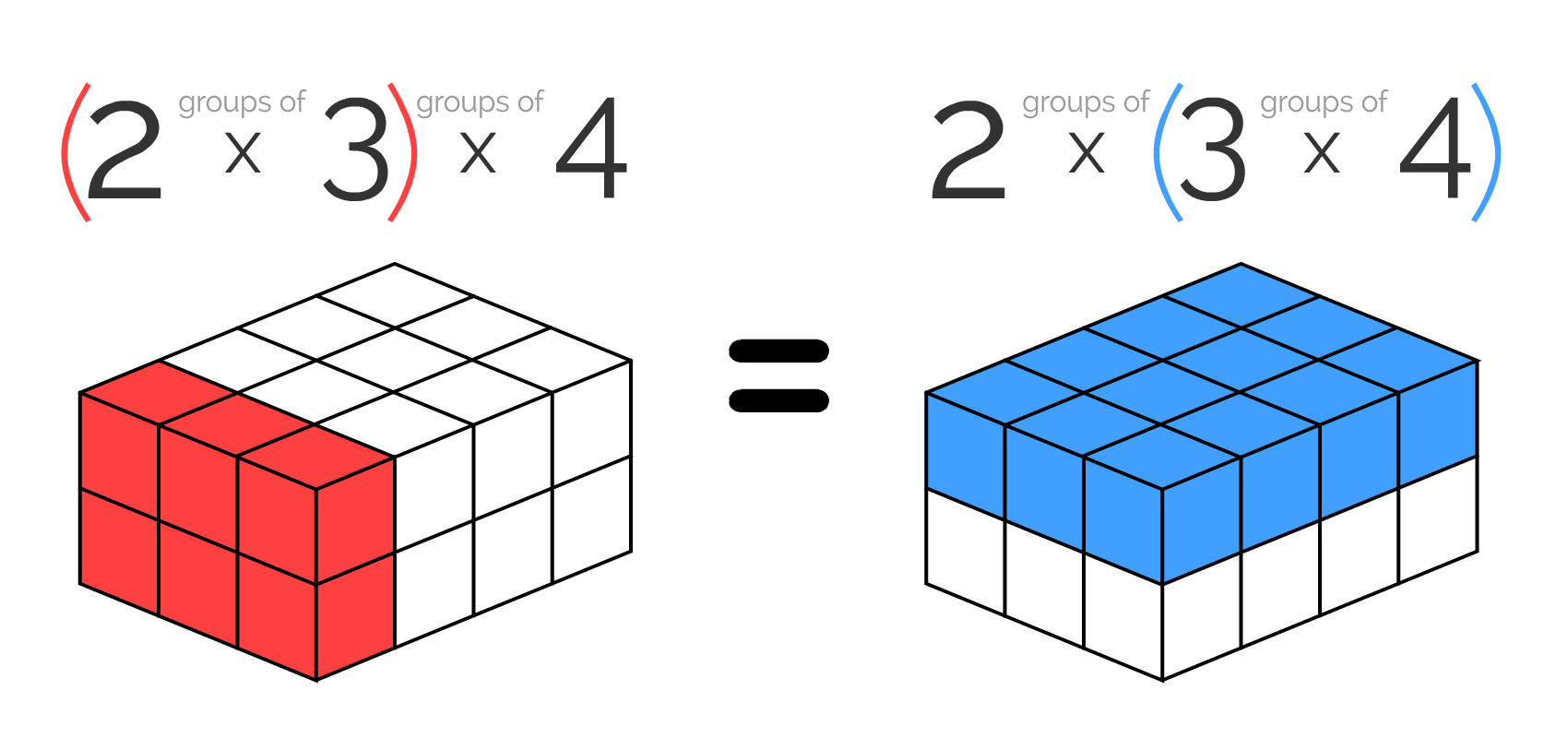
3. A formal university-level proof, for why if associativity holds for multiplying 3 numbers, then it holds for any multiplying [any number of] numbers.

But: there's no fully visual proof for the associativity of multiplication for more than three whole numbers.

Until I found one!

As far as I know, this visual proof is novel? I was hoping to save the grand reveal of this proof for my book that I may or may not ever write. But, it's been sitting in the closet of my mind for two years, so let's just get it out:

The Proof:

First recall, what do brackets mean in math? It means: "do this first".

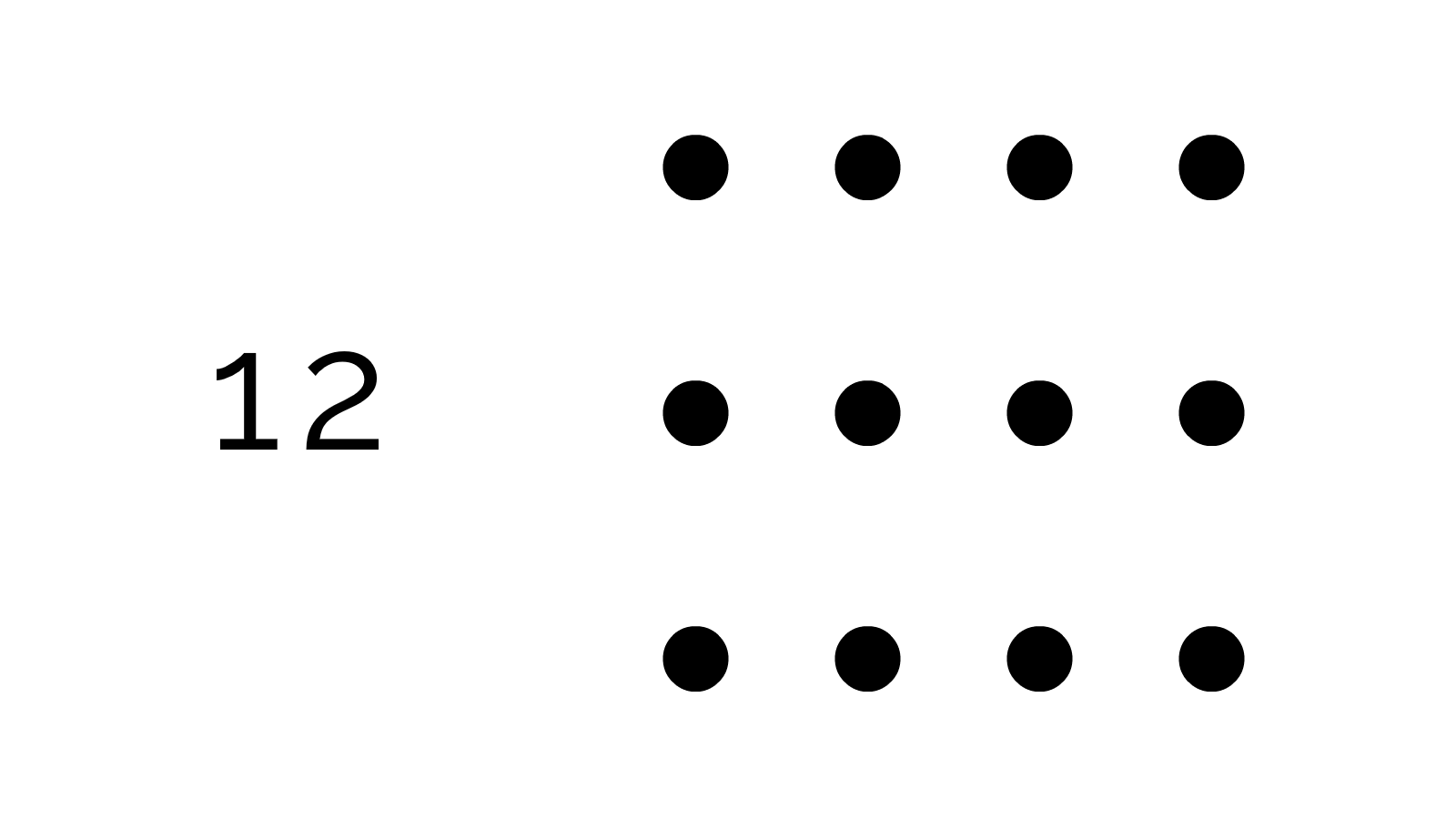
Now, how can we visualize multiplication? Remember "3 times 4" means "3 groups of 4". Like, 3 boxes of 4 balls each:

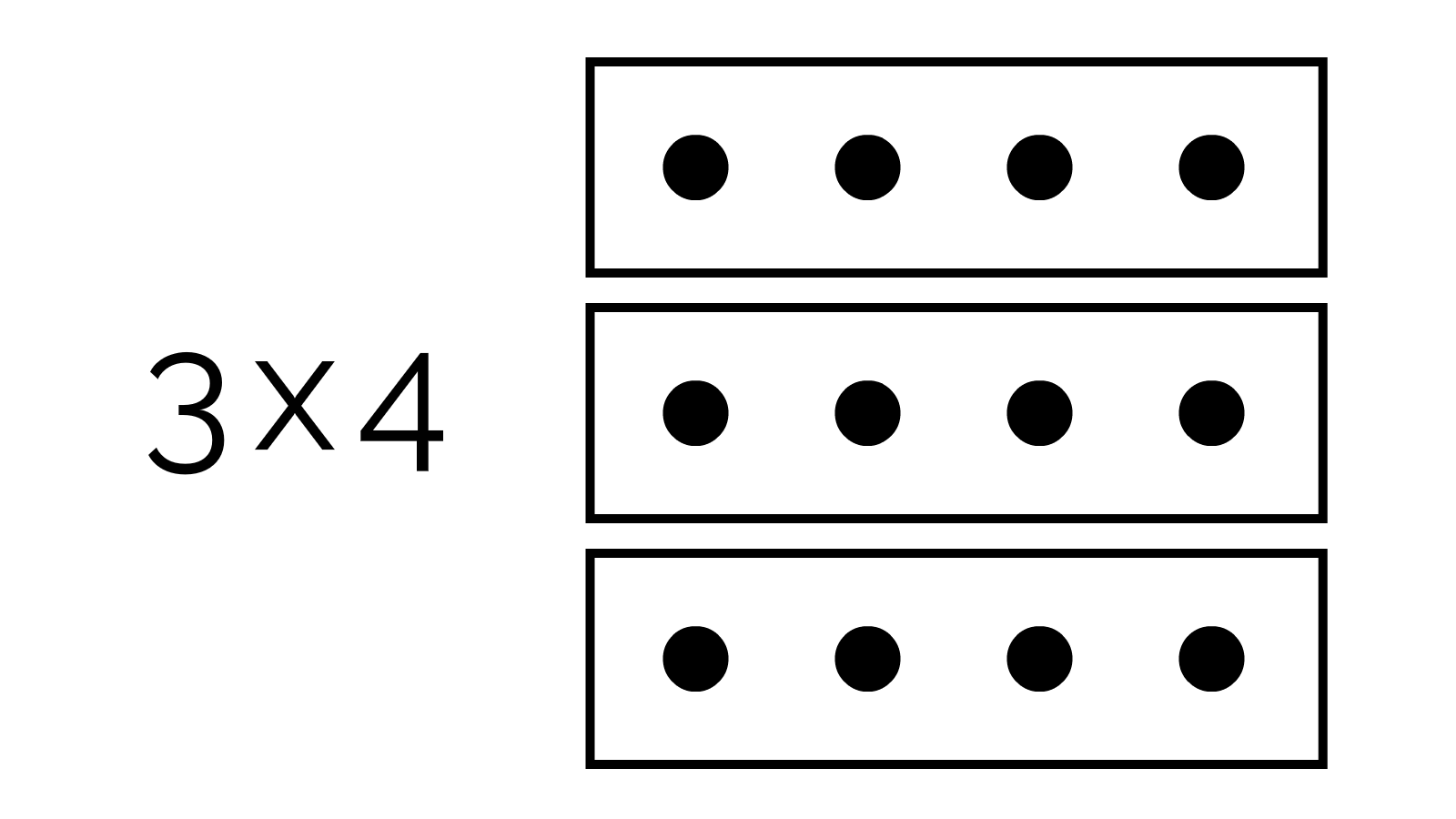
Then, "doing" a multiplication means removing the box containers:

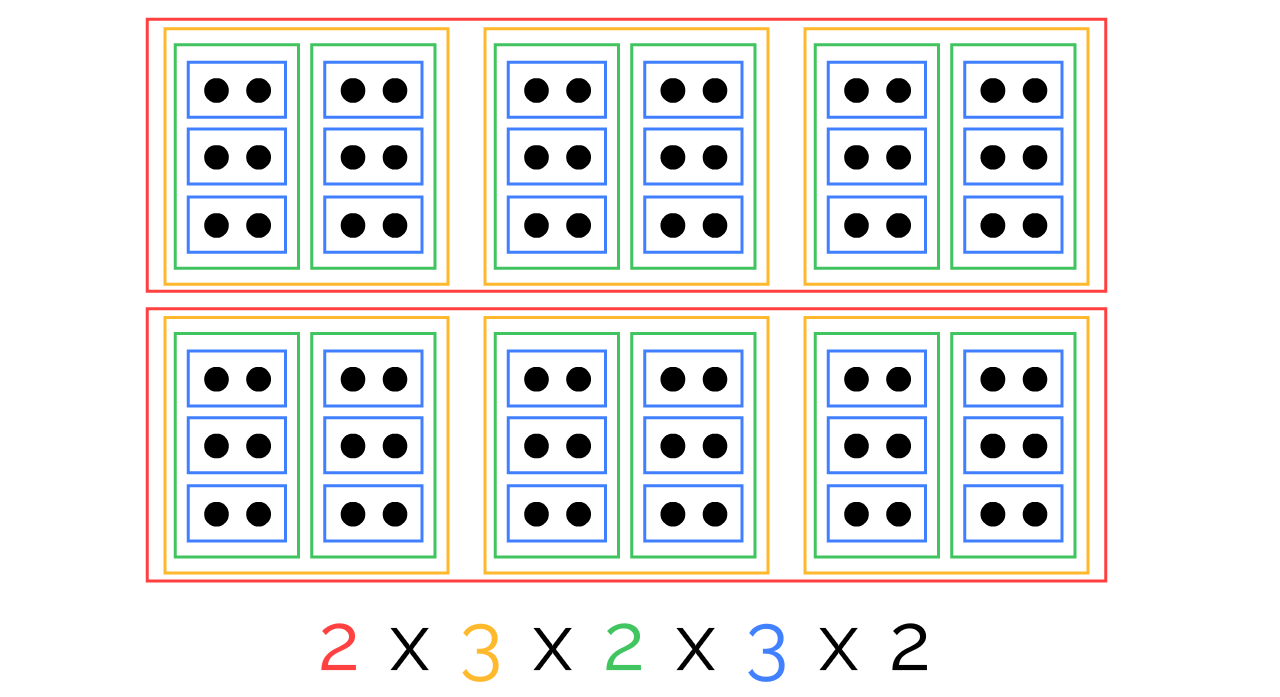
Now, let's picture 2 x 3 x 4. That's 2 boxes of 3 boxes of 4 balls each:

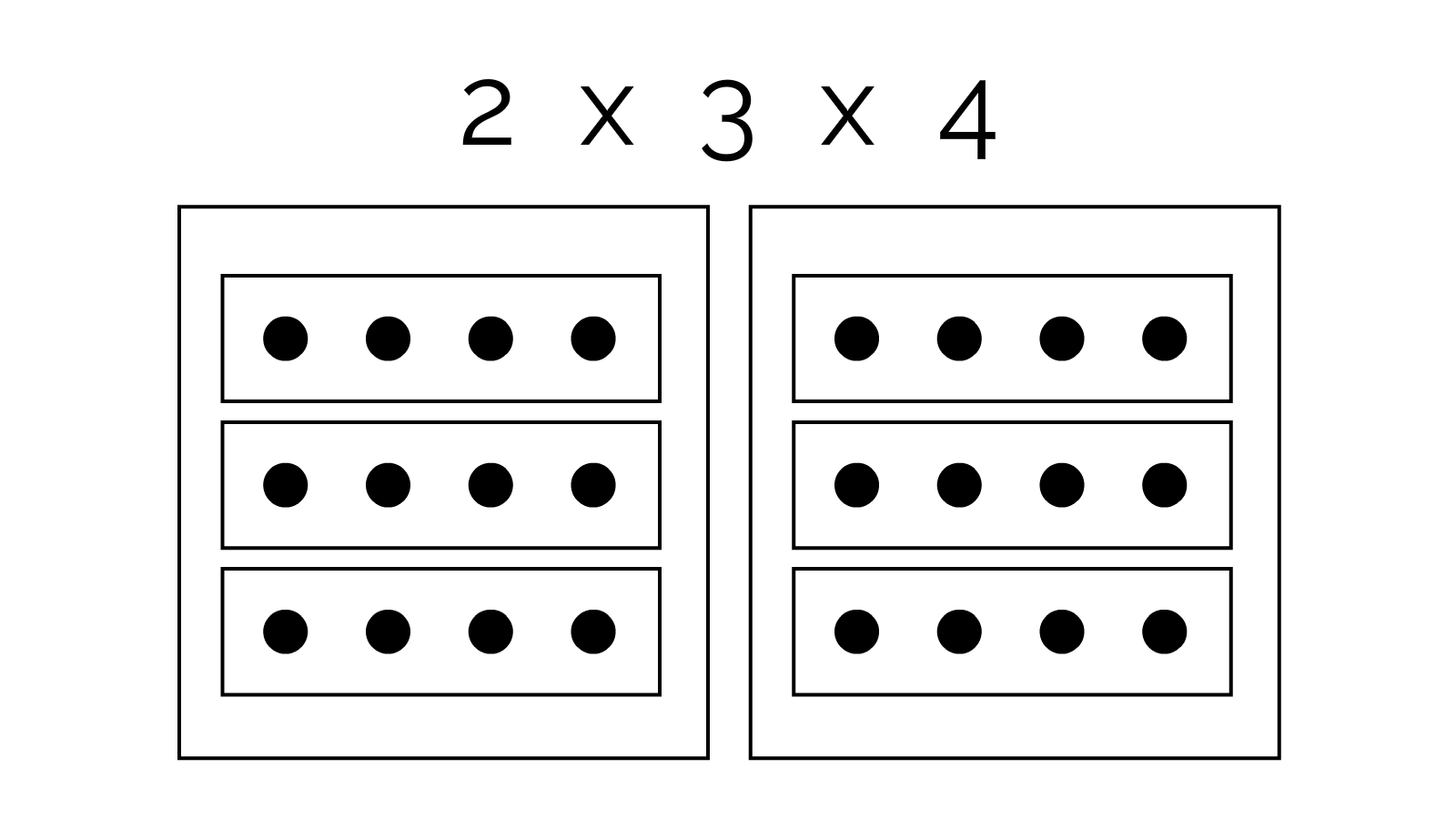
Since doing a multiplication means removing a box container, it should now be clear: it does not matter which order you remove the box containers, you'll always end up with the same number of balls.

In other words, it doesn't matter which multiplications you do first.

In other other words, brackets don't matter in multiplication!

Best of all, with this visual, we don't need the university-level proof: we can instantly see that associativity must be true for multiplying any number of numbers!

Here's 2 x 3 x 2 x 3 x 2, bracketed in three different ways, all leading to the same result:

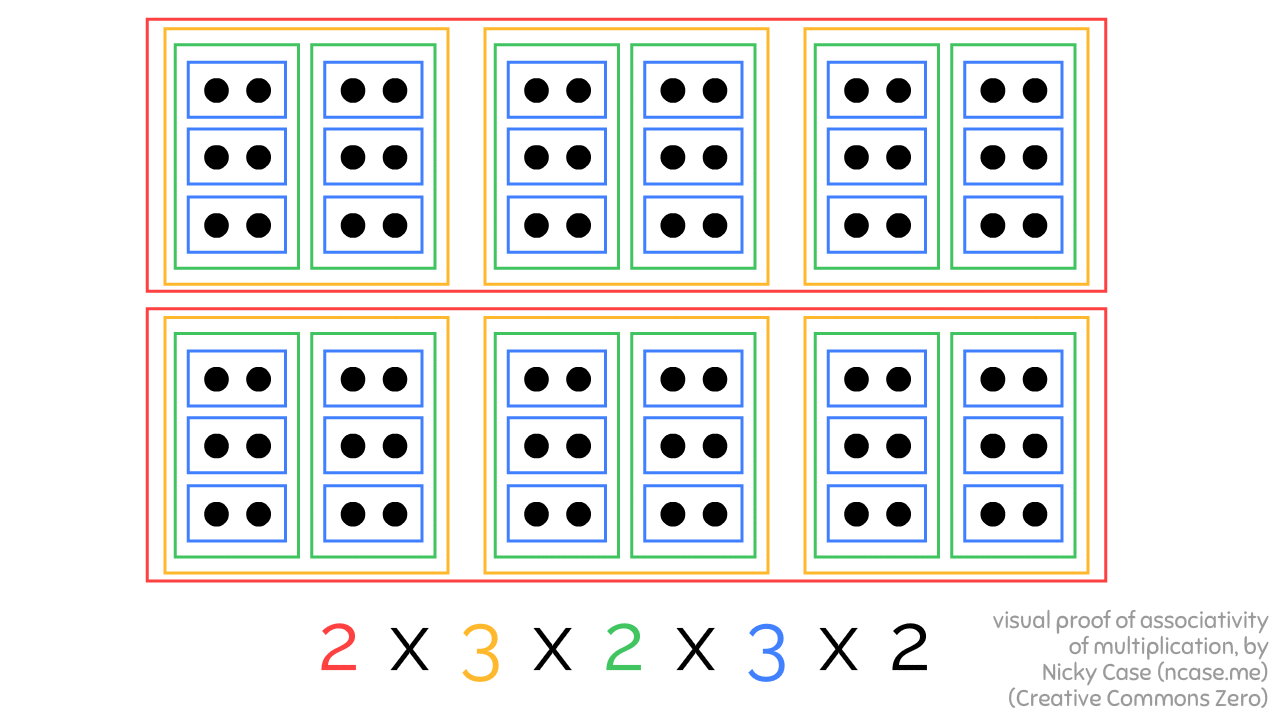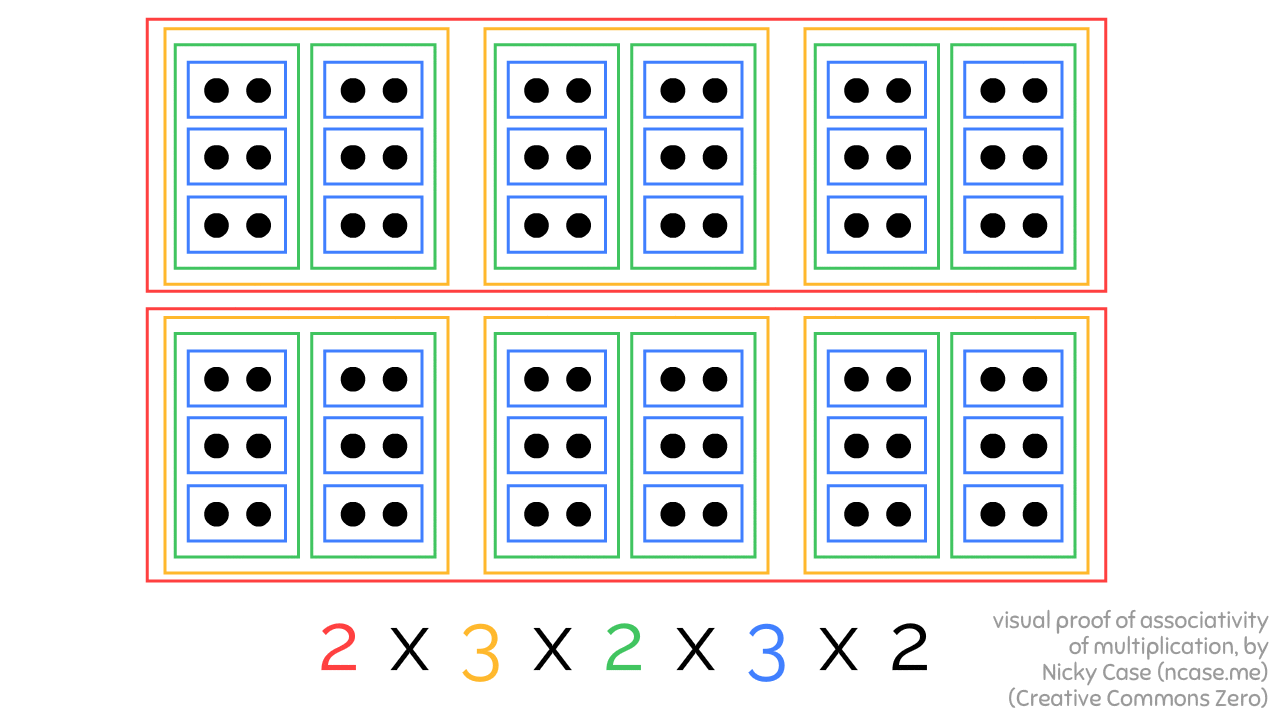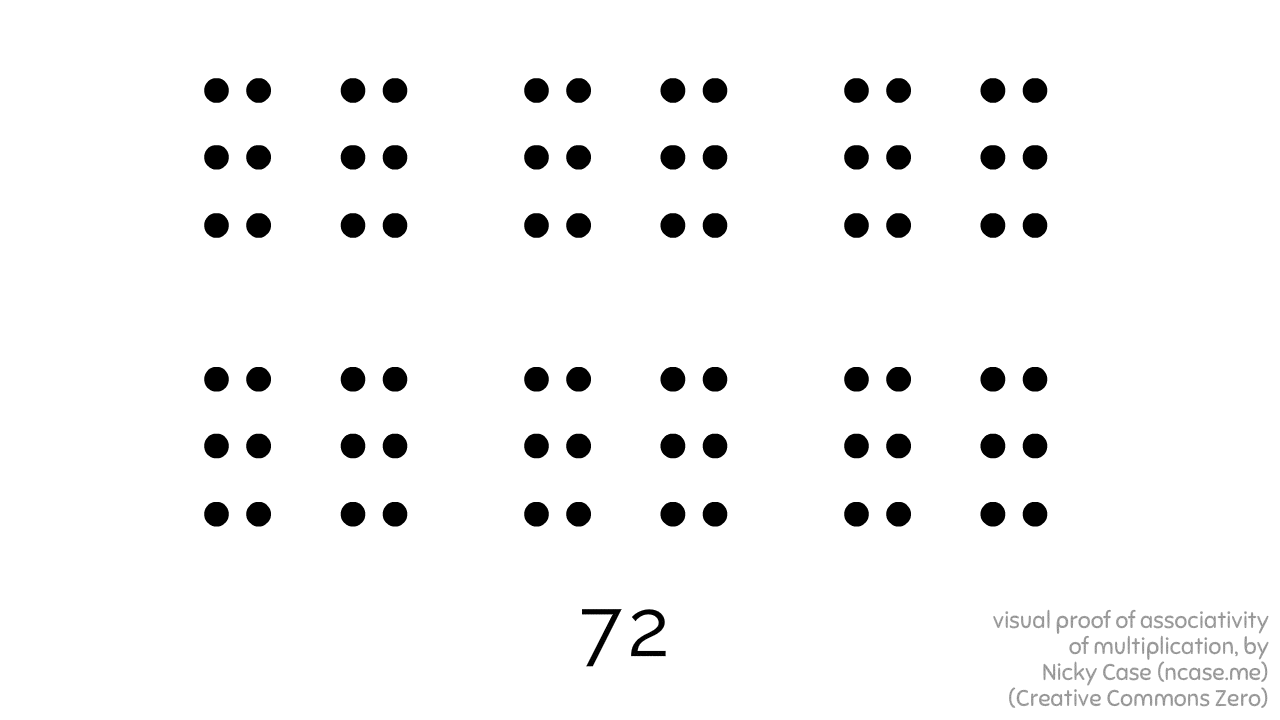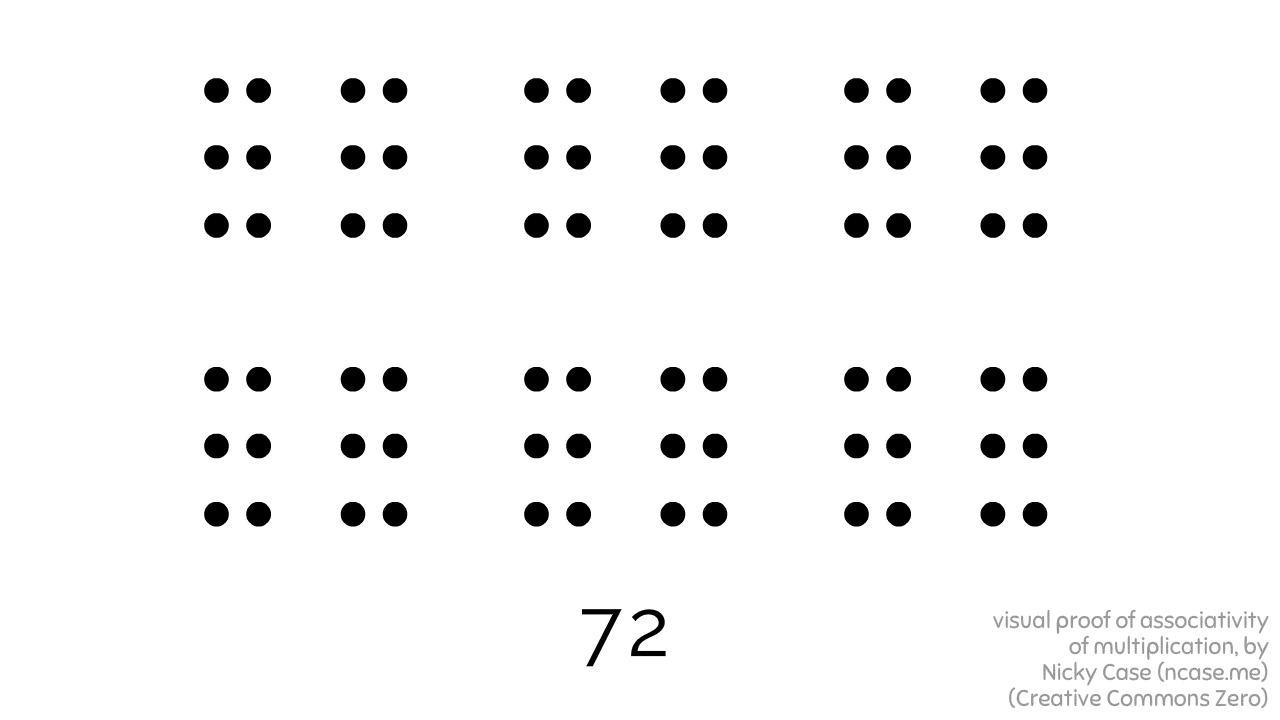
Granted, this proof only works for whole numbers... but still! Kinda shocking a visual proof of such a basic fact did not exist before!

What's left to do:

• Visual proof of "Order doesn't matter (commutativity) for more than two numbers."
• Visual proof of "For any operator, not just whole-number multiplication: if it's associative for 3 numbers, then it's associative for 3+ numbers."

But I guess you'll have to wait until I write that book, to see those. (Or, wait until I get bored and just dump them as standalone articles.)

This blog post is a standalone section, ripped out of my 90-minute-long[!!!] blog post, Cleaning Out The Idea Closet (47 Projects on My Backlog).